Tal vez el aspecto más importante a considerar en estos dos
temas es cuando y en qué extensión enseñar a derivar e integrar. Ya que es
frecuente encontrar alumnos que tienen serias dificultades a nivel de universidad
por no recordar bien como integrar. Es importante evitar esta situación en la
medida de lo posible, así como asegurar que el alumno no llega al final del
bachillerato sólo para hacer un esfuerzo supremo por aprender integrales
(suponiendo que se enseñe en el último trimestre).
En cualquiera de los casos nos referimos a cursos de Matemáticas
Aplicadas a las Ciencias, ya que es la rama en la que mayor tiempo y profundidad
se toma para enseñarlas.
DERIVADAS:
Aunque es frecuente encontrar profesores que deciden enseñar
a derivar desde 4º ESO funciones muy sencillas, se ha comprobado que a tales
edades resulta innecesario, ya que no es lo bastante complicado como para
necesitar una preparación previa al bachillerato en dicho curso y por el
contrario, supone una carga y gasto de tiempo importante, que puede resultar
completamente superflua para el alumno que no realizará bachillerato.
En cuanto a 1º de bachillerato, el alumno debe saber derivar
perfectamente cualquier función relacionada con el resto del temario de
bachillerato, esto significa que no es necesario enseñar a derivar funciones
tales como senos hiperbólicos, etc. Por otra parte hay que recordar que el
alumno está destinado a saber derivar sin usar una tabla, que no debería usarse
en el examen y esto es también otra razón para no enseñar a derivar más
funciones de las que puede recordar.
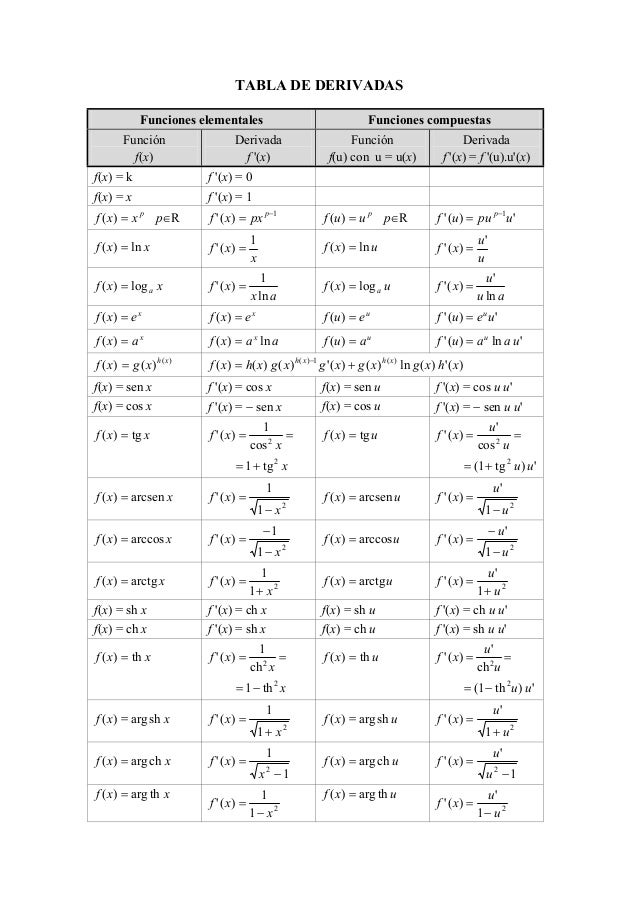
La enseñanza de este tema no suele tener especiales
complicaciones si el alumno lo aborda de una manera mecánica. Aún así, se
recomienda hacer especial hincapié desde lo antes posible en la importancia de
la regla de la cadena. La inmensa mayoría de los fallos en lo que se refiere a
derivadas están causados por no seguir la regla de la cadena. Por otro lado no
debería gastarse más tiempo del debido en enseñar la definición de derivada, ya
que para la mayoría de alumnos resulta un concepto demasiado abstracto como
para recordarlo y de difícil aplicación práctica.
Durante el curso de 2º de bachillerato el alumno ya debería
saber derivar y sólo debería dedicársele un repaso. Por otra parte, en este
curso es necesario abordar el tema de las optimizaciones, por lo que es
conveniente comprobar que el alumno recuerda cómo derivar funciones sencillas.
Como excelente colección de derivadas con soluciones
encontramos: http://www.derivadas.es/ especialemente el apartado de derivadas más difíciles.
INTEGRALES:
Las integrales indefinidas tienen fama de ser el tema que
más complicado ve un alumno, una evidencia de que tal vez esto es cierto es que
en comparación con las derivadas en las que se disponía de una tabla, en las
integrales una tabla no puede aportar todas las reglas para integrar funciones.
Además es un tema no precisamente breve.
Por todo ello, tal vez la mejor solución al problema es
enseñar a integrar funciones desde 1º de bachillerato. No es necesario enseñar
a hacer integrales definidas, ni dar en toda su extensión las integrales
indefinidas (lo ideal es no ver las integrales por partes y las integrales
racionales), pero está comprobado que si el alumno vio las integrales durante
dos cursos diferentes el tema se vuelve mucho más abordable. Y tal vez más
importante: el alumno recordará con mayor claridad a nivel de universidad cómo
integrar. Otra ventaja añadida es que el temario de 2º de Física está repleto
de integrales que se pueden enseñar con facilidad si el alumno sabe integrar
desde el primer curso.
Como excelente colección de integrales resueltas disponemos de:
el compendio de 801 integrales resueltas, este famoso compendio resuelve ejemplos de ejercicios de publicaciones bien conocidas y resulta de utilidad y eficacia hasta en el ámbito universitario. Tal vez una de las mejores herramientas académicas en cuanto a integrales se refiere.
Para ver contenidos más diversos disponemos de este blog: dedicado a las integrales
CONCLUSIÓN/RECOMENDACIÓN: Asegurar un perfecto aprendizaje
de las derivadas e incorporar las integrales al temario de 1º de bachillerato.